Introduction
The basis of this experiment is to determine the heat of reaction from the temperature dependence of equilibrium constant. The reaction basically involves dissolving borax Na2B4O7.10H2O in water. Borax is sparingly soluble in water and its solubility properties is calculated at different temperature .Quantities like enthalpy ∆H0, the entropy ∆S0, free energy ∆G0 as well as Ksp are determined for the reaction system.
Saturated solution of borax are to be obtained, then it is subjected to further analysis. This makes the concentration of solid borax constant. The equilibrium borate ion is obtained at different temperature by titration with standardized 0.5M HCl of the saturated solution and the solubility product determined at various temperatures.
Ksp of borate ion should be calculated at different temperatures and the complete thermodynamic parameters for dissolution of borax ion in water obtained.
Theory
Temperature: In science, temperature is a physical property of a system that underlines the common notions of hot and cold. Temperature is one of the principal parameters of thermodynamics.
Equilibrium and Equilibrium Constant: Equilibrium is a state at which the rate of appearance of product equals the rate of disappearance of reactants. Equilibrium constant on the other hand is represented by a constant K, which is the numerical value obtained when we substitute actual equilibrium concentrations into equilibrium expression.
It can be represented by the expression below by considering the reaction below;
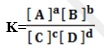
Where
K = equilibrium ,
[ ] = concentration
In writing the solubility product constant expression for borax in water, water is removed from the equilibrium expression, this is simply because the water in borax is lost to mixture of sample and the water added to the borax is just to prepare a saturated solution of it for titration and this does not change the original amount of water in borax. The determination of a value for solubility product was able to tell the amount of the borate ion in the sample mixture. This made it easy to express Na+ in terms of B4O5(OH)42-. So it was possible to express Ksp in terms of concentration of borate ion.

K for this reaction is written as [Na+]2 [B4O5(OH)42-]
Since [Na+] = [B4O5(OH)42-],
K= 4[B4O5(OH)42-]3
If we find the concentration of borate ion at any temperature, this equation will help us to directly find the solubility product at that temperature.
Borate ion will react with the acid (HCl) in a ratio of 1:2
B4O5(OH)42-(aq) + 2HCl(aq) + 3H2O(l) → 4B(OH)3(aq) + 2Cl–(aq)
nHCl = volume of HCl used (in litre) x Molarity of HCl
This helps us in determining the no of moles of borate ion& hence its concentration at any particular temperature. This process is repeated for borate ion containing sample obtained at various temperature hence solubility product at different temperature was calculated. The expression that relates equilibrium constant K, Free energy ∆G0, Heat change ∆H0 and the entropy of the reaction ∆S0 is
∆G0 = -RTInK = ∆H0 – T∆S0
Where
T-temperature in Kelvin and
R=gas constant (8.314Jmol-1)
The following equation can be arranged linearly as
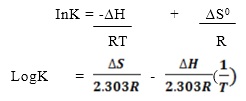
According to this equation, a plot of LogK in the Y-axis and 1/T on the X-axis gives a straight line graph and the slope is -∆H0/(2.303R) . Hence ∆H0 and ∆S0 can be calculated. This experiment is aimed at determining solubility of borax at different temperature. Sample of saturated borax are collected at five different temperatures and this is a saturated solution and it is titrated against HCl using bromocresol green as indicator and it gives a golden yellow coloration at its end point.
Reagents and Apparatus
1. 0.5M HCl solution
2. Bromocresol green indicator
3. Water
4. 30g borax
5. Burette
6. Test tubes
7. 150ml & 400ml beakers
8. Thermometer.
Procedures
1. Weigh 5.0ml of water into each of 5 test tubes and the water level was noted with each tube labeled 60o, 50o, 40o, 30o, 20o.
2. Weigh the 30g borax into a 150ml beaker, 50ml of water is added and the solution heated to about 65oC.
3. After complete dissolution of the borax, a little of the borax is again added to saturate the solution.
4. Allow the solution to cool to 60oC while stirring it with the thermometer.
5. At this 60oC temperature, the mixture is allowed to settle and 5.0ml of the solution should be decanted into the test tube marked 60oC.
6. Transferred the content from the step above into a 400ml beaker and warm the solution to dissolve the crystallized borax.
7. Then titrate the solution against a standardized 0.5M HCl using 3drops of bromocresol green as indicator.
8. Further cool the saturated solution to temperatures 50, 40, 30, and 20oC respectively and repeat steps (5)-(7) for each solution.
Results and Calculations
- The titration result is tabulated as shown below:

- Calculate the number of moles of borate ion and subsequently its concentration for each temperature. From this result, then calculate the value of the equilibrium constant K for each. Tabulate the result as shown below:
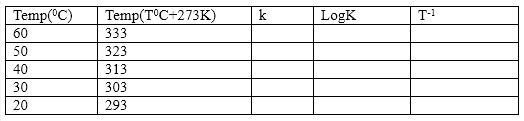
- Plot a graph of Log K against T-1
- Take two points P & Q with their respective logK and T-1 values P(LogK1, T-11) and Q (LogK2, T-12)
- By formula,
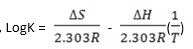
- Solve eqns (i) and (ii) simultaneously to get values for ∆S and ∆H.
Discussion and Conclusion
From this experiment, it can be observed that thermodynamic quantities can be determined experimentally with high level of accuracy in the laboratory using a suitable indicator whose equilibrium is temperature dependent.
References
- V Majer, J Sedelbauer and Wood, “Calculations of standard thermodynamic properties of aqueous electrolytes and non-electrolytes.
- P.W Atkins, Physical chemistry 1st edition, Oxford University press.
Download “Report - Determination of Heat of Reaction”
Download “Procedure - Determination of Heat of Reaction”